El objetivo de nuestro trabajo

El objetivo principal del trabajo es caracterizar la transición de estado ordenado (magnetizado) a estado desordenado (desmagnetizado) para valores altos de la concentración de átomos magnéticos, en los que el tipo de la transición de fase pasa de ser de primer a segundo orden. La localización del valor exacto de la dilución a la que esto ocurre, así como los exponentes críticos de la zona de transición de segundo orden, es una tarea de gran interés y completamente inabordable hasta ahora.

Cuando el sistema es completamente puro, al disminuir la temperatura se produce una transición de fase análoga a la que ocurre al enfriar el agua. Técnicamente se denomina una transición de fase de primer orden (más información en inglés en http://en.wikipedia.org/wiki/Phase_transitions). Al igual que la transición de fase entre el agua y el hielo, alrededor de la temperatura donde ocurre la transición de fase puedan "coexistir" ambas fases (sin embargo una de ellas no es estable y tenderá a desaparecer, aunque eso puede durar mucho tiempo): por ejemplo hielo flotando en el agua cuando la temperatura es mayor de 0 grados (recordad el Titanic!!).

Conforme desordenamos el sistema, la transición de fase de primer orden se va debilitando (por ejemplo, la región en temperaturas donde pueden "coexistir" ambas fases se va reduciendo) y finalmente desaparece el carácter de primer orden en la transición: la transición pasa a ser de segundo orden donde ya esta prohibida la coexistencia de las dos fases. Un ejemplo de este tipo de transición se da en los imanes, por ejemplo de Hierro.

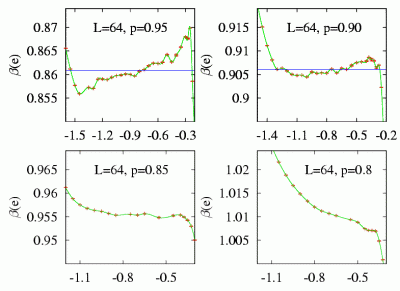
Para caracterizar la coexistencia de fases (y las transiciones de fase de primer orden) se puede usar la llamada construcción de Maxwell (famoso físico escocés, más información biográfica en http://es.wikipedia.org/wiki/James_Clerk_Maxwell). Para realizar dicha construcción se representa la temperatura del sistema frente a su energía interna (en la gráfica adjunta en concreto se representa la inversa de la temperatura en función de la energía por átomo).

Cuando la gráfica presenta una "joroba" en la parte central es fácil definir la temperatura a la que ocurrirá la transición de fase (la temperatura crítica). Para ello usamos el hecho de que a la temperatura crítica el sistema debe tener la misma probabilidad de estar en el estado ordenado que en el desordenado. A una temperatura fija (línea horizontal en la construcción de Maxwell) la probabilidad de estar en un estado energético concreto está relacionada con el área encerrada entre la línea horizontal y la construcción de Maxwell. Por lo tanto, se define la temperatura crítica como aquella que encierra el mismo área a ambos lados de la curva.

Además, en la construcción de Maxwell se define el calor latente (energía que hay que suministrar al sistema para que se produzca completamente el cambio de estado) como la distancia entre las energías de corte con la línea de temperatura crítica más a la derecha y más a la izquierda. Además la tensión superficial (relacionada con la energía que "se necesita" en formar una interfase) se relaciona con el área bajo una de las dos jorobas de la construcción de Maxwell.

A simple vista en casi toda la construcción se puede observar cómo la temperatura de sistema crece conforme aumenta su energía interna (¡lógico!), ésto no ocurre sin embargo en la parte central, estas energías corresponden a un sistema en un estado termodinámicamente inestable (la famosa "coexistencia" donde solo una de las fases es estable). Una vez definida la temperatura crítica pueden observarse estados del sistema con temperatura mayor (o menor) que la temperatura critica, son los llamados estados metaestables. En dichos estados existe coexistencia entre el estado ordenado y desordenado (recordad a Leo diCaprio) aunque solo uno de ellos es estable.

Concretando para las gráficas adjuntas: cada una corresponde a un sistema de 64³ espines con distinta concentración de impurezas. El valor L es la longitud lineal del sistema mientras que el valor de p es la concentración de átomos magnéticos (en tanto por uno). Las diferentes gráficas corresponden a muestras individuales (diferentes localizaciones de las impurezas) tomadas al azar.

En estas gráficas puede verse cómo la energía deja de tener los picos de máximo y mínimo (la joroba) conforme se aumenta la concentración de impurezas. Es decir se observa claramente que para este tamaño de red llegamos a una concentración de impurezas crítica (alrededor del 15%, un valor de p=0.85) en la que el calor latente y la tensión superficial se anulan (claro indicativo de que se está realizando una transición de segundo orden).

Esto está claro un sistema de 64³ (aprox. 3·10⁵) átomos, pero ¿ocurrirá lo mismo en un sistema más grande? ¡Recordad que un sistema macroscópico tiene del orden de 10²³ átomos! Para dar resultados aplicables a sistemas grandes tenemos que ver cómo varían los observables conforme varia el tamaño del sistema. De ahí que estas simulaciones se estén llevando a cabo en sistemas de diversos tamaños.

Actualmente con Ibercivis se está realizando un barrido para varios valores de la concentración de átomos magnéticos (0.7 < p < 0.95) tomando 500 muestras para cada valor de p, para sistemas de tamaños L=32 y L=64. Las simulaciones posteriores pretenden alcanzar sistemas de hasta L=128 y a unas 5000 o 10000 muestras para cada valor de p. Se pretende hacer un barrido que incluya sistemas de 32³, 48³, 64³, 96³ y 128³ espines. Si se obtienen del orden de unas miles de muestras para estos sistemas en los valores de la dilución más interesantes se habrá obtenido una visión del fenómeno de una calidad jamás alcanzada.